❀ 題目傳送門 ❀

https://atcoder.jp/contests/dp/tasks/dp_f

❀ 解題小技巧 ❀

參考文章

可以參考我的另一篇基因序列密碼

推薦一篇很讚的文章

前言

在我的上一篇 LCS 文章(基因序列密碼)中，用的是比較偷機的技巧
可以使用的原因是因為該字串最大長度較小
原先我想使用上次的 code，結果發現會爆炸
因此本篇主要探討 dp 中最常字串是怎麼來的

正題

核心觀念

首先先觀察，如果兩字串長度皆為 1（稱為 1,1 情況），策略會是什麼

如果字串一樣，則最大長度為一
如果字串不一樣，則最大長度為零

再來觀察，如果一字串長度為 1 一字串長度為 2 （稱為 1,2 情況），策略會是什麼

如果最後一個字串一樣，則最大長度為一
如果最後一個字串不一樣，則變為（1,1）情況

最後觀察，如果兩字串長度皆為 2，策略會是什麼

如果最後一個字串一樣，則變為（1,1）情況
如果最後一個字串不一樣，則變為（1,2）與（2,1）情況

轉移式

因此我們可以寫出（n,n）情況的轉移式

1
2
如果最後一個字串一樣，則變為（n-1,n-1）情況
如果最後一個字串一樣，則變為（n,n-1）與（n-1,n）情況

也就是

1
2
if (s1[i-1] == s2[j-1]) dp[i][j] = max(dp[i][j], dp[i-1][j-1] + 1);
else dp[i][j] = max(dp[i-1][j], dp[i][j-1]);

其中 dp[i][j] 的 i 代表字串一的長度（上面的第一個 n），j 代表字串二的長度（上面的第二個 n）

最長字串是怎麼來的？

dp，其實就是一個大矩陣，因此把表格畫出來看看

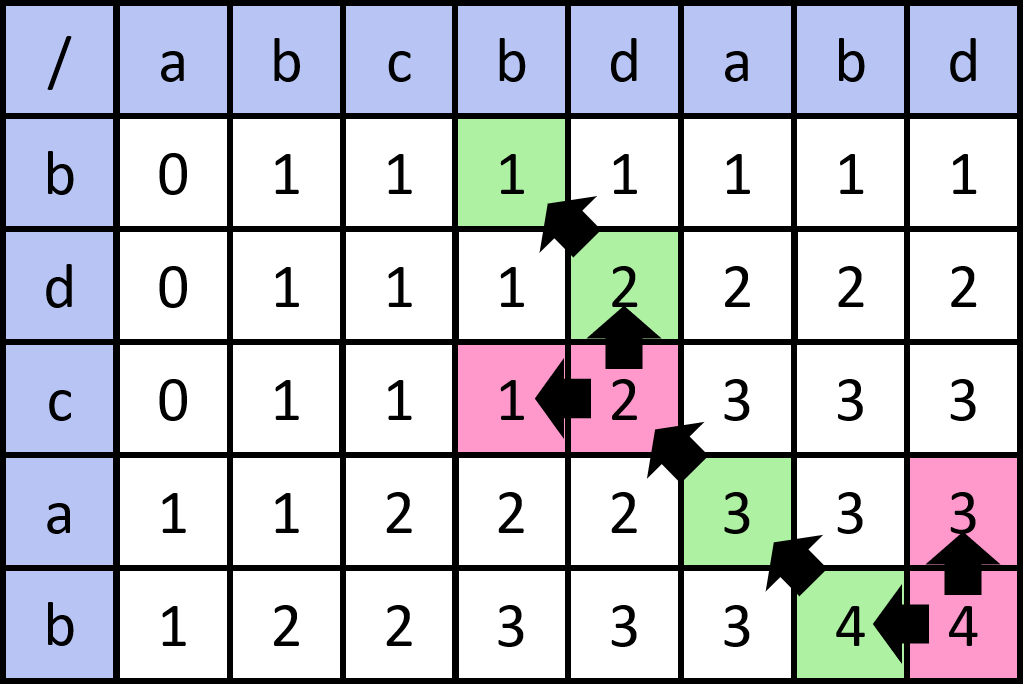
（n,m）情況下，如果 s1[n] == s2[m] 則知道 dp[n][m] 值是由 dp[n-1][m-1] 推來的
如果 s1[n] != s2[m] 則知道當前 dp[n][m] 值是由 dp[n-1][m] 或 dp[n][m-1] 推來的

❀ 參考程式碼 ❀

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <bits/stdc++.h>

#define starburst ios_base::sync_with_stdio(false), cin.tie(0), cout.tie(0);

using namespace std;

int dp[3005][3005];

int main() {
  starburst
  
  string ans = "";
  string s, t;
  cin >> s >> t;

  memset(dp, 0, sizeof(dp));
  
  for(int i = 1; i <= s.length(); i++){
    for(int j = 1; j <= t.length(); j++){
      if (s[i-1] == t[j-1]) {
        dp[i][j] = max(dp[i][j], dp[i-1][j-1] + 1);
      }
      else {
        dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
      }
    }
  }
  
  int i = s.length(), j = t.length();
  while (i && j){
    if (s[i-1] == t[j-1]) ans += s[i-1], i--, j--;
    else if (i > 0 && dp[i-1][j] >= dp[i][j]) i--;
    else j--;
  }
  reverse(ans.begin(), ans.end());

  cout << ans;
  return 0;
}